Hey helpers! Today we logged on into CP Armies for our Operation Prosperity! It included the Iceberg, Snow Forts and the Stadium led by Riley, Rooboo and Monika respectively! The event had amazing tactics and formations! Good job Helpers!
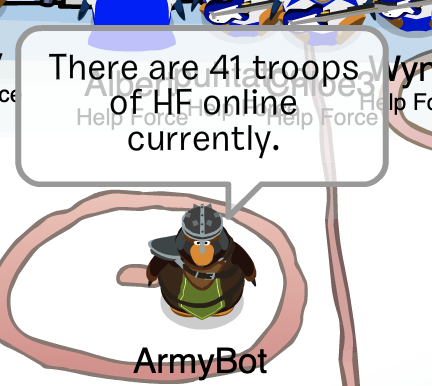
Max: 41+
Comment below for Promotions!

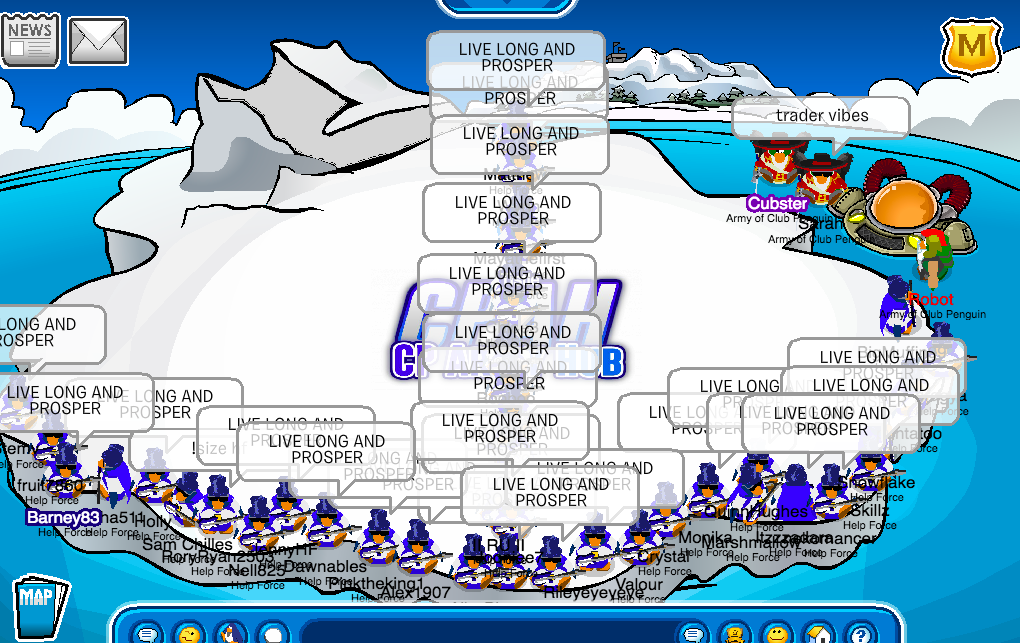
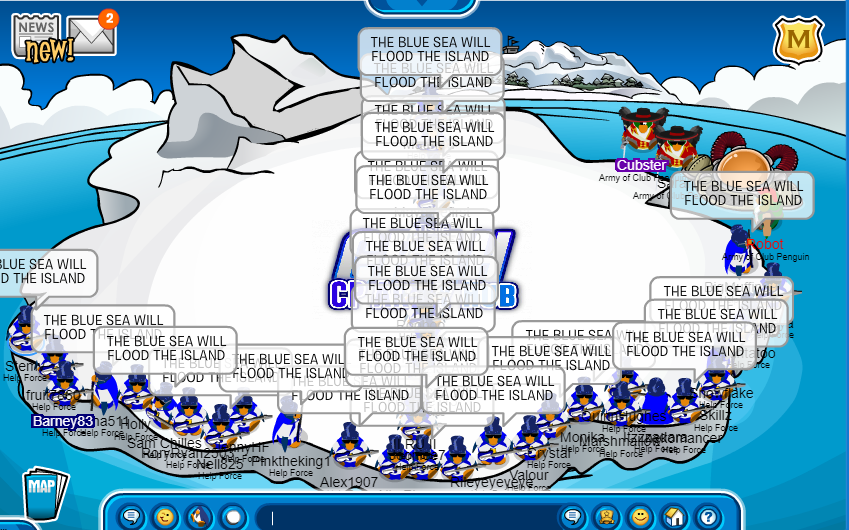
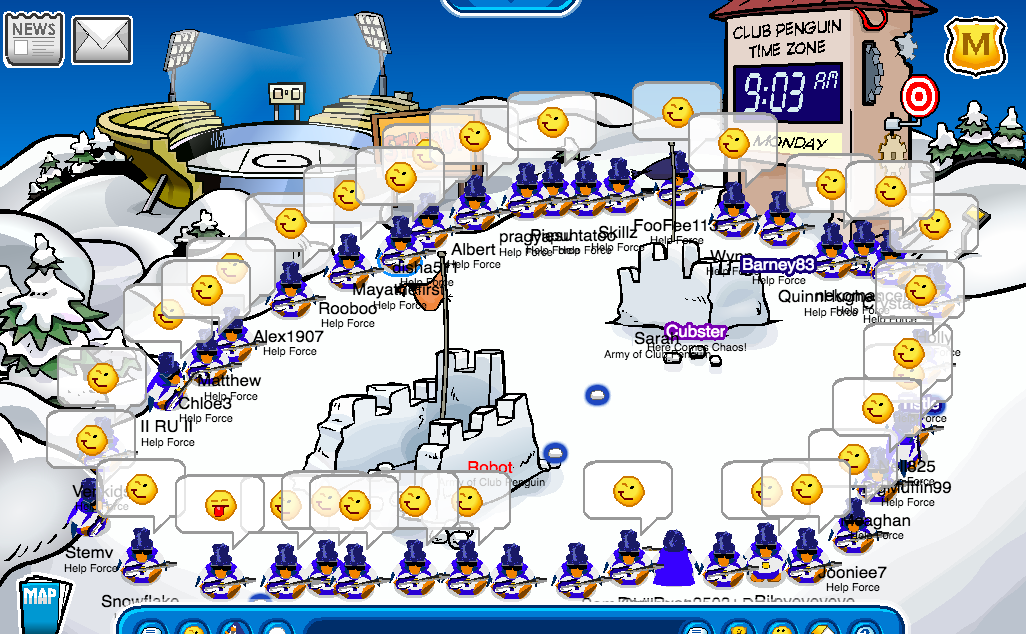
Unleash The Power Of Helping!
Filed under: Event Posts, Help Force CP, Official Events















pinktheking1-i came
I attended! Thank you for hosting!!
Penguin name – disha511
Discord – Disha#2388
It was amazing and full on prosperous lmao <3 Thank you for hosting guys ^_^
awesome event, very prosperous…😂thanks for hosting! attended as Chloe3
Penguin Name : II RU II
Discord : Ru#8072
I attended.
Discord- Valour#0849
CPA- Valour
Penguin Name : Albert
Discord: ¡albert!#2310
CPA name-BigMuffin99 discord-BigMuffin69
Wit sorry dicord- wombat99#7381
I attended!! And it was amazing!! Ty for hosting!!
-Pragya
I came!
In game name: VInjVaccine
Discord: Vaccine Injured Vaccine #4700
I attend!
Peguin name: Mayathefirst
Discord: Mayathefirst#7505
I came, great event
penguin name: Ireco
Discord: Ireco#7131
i attended! ty for hosting!
discord: alex1904
cpa: alex1907
My discord user is Jenny!! ;)#0451 😀 and my cpa username was JennyHF!!
i attended! ty for hosting!
discord: stemv#5882
cpa: stamv
I attended
CPA Name: Jooniee7
Discord Name: Joonieee7
Hi! I attended the event! TY for hosting!.
Thank YOU so MUCH for Hosting, Give me my ping please Snowfalke-Soft.
i attended ty for hosting
I came!
Thanks for hosting! HFBF!💙
Ty for hosting!
I attended
I cam- *has a stoke again* eughghghgh -Skillz btw
Foofee was there too!
CPA: FooFee113
Discord: Joe | Foo
Great event! Thank you for hosting! <3
I was there. Thanks for hosting.
I attended!
Discord: Venkids
CPA: Venkids
I attended this event!
I was there! Meaghan is my username on both